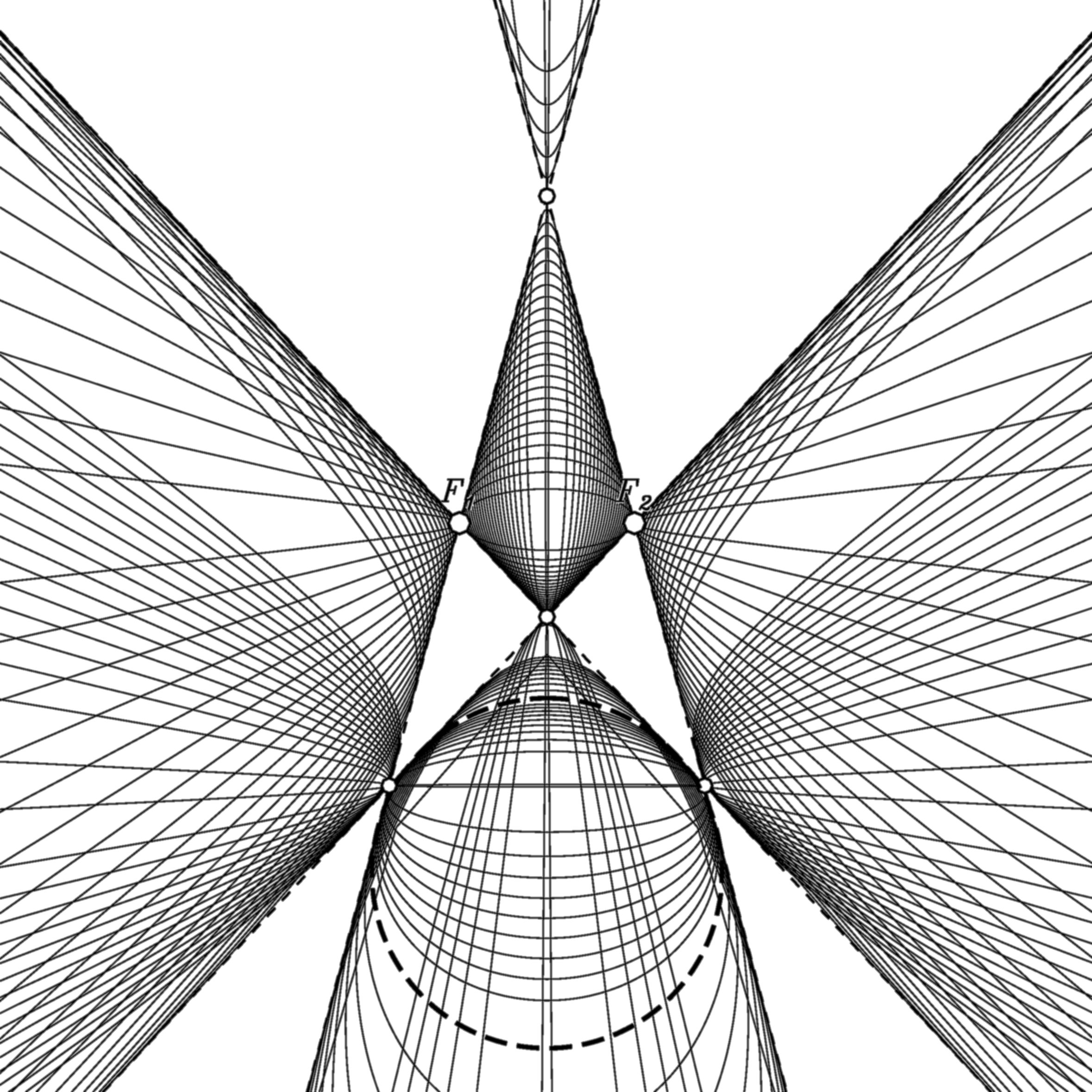
Confocal conics in deSitter geometry
We see a family of conics with four common tangents. (One of these conics may serve as the absolute one.) The six vertices of the quadrangle of common tangents present the common foci of the family: Given a line g through one of the foci, the poles P[g] produced by the family are collinear. This line p of poles divides with g the two tangents through the focus harmonically. This generalizes the euclidean observation that the pole of a line through a focus lies on the perpendicular to the line in the focus.| Kapitel Portal |


|