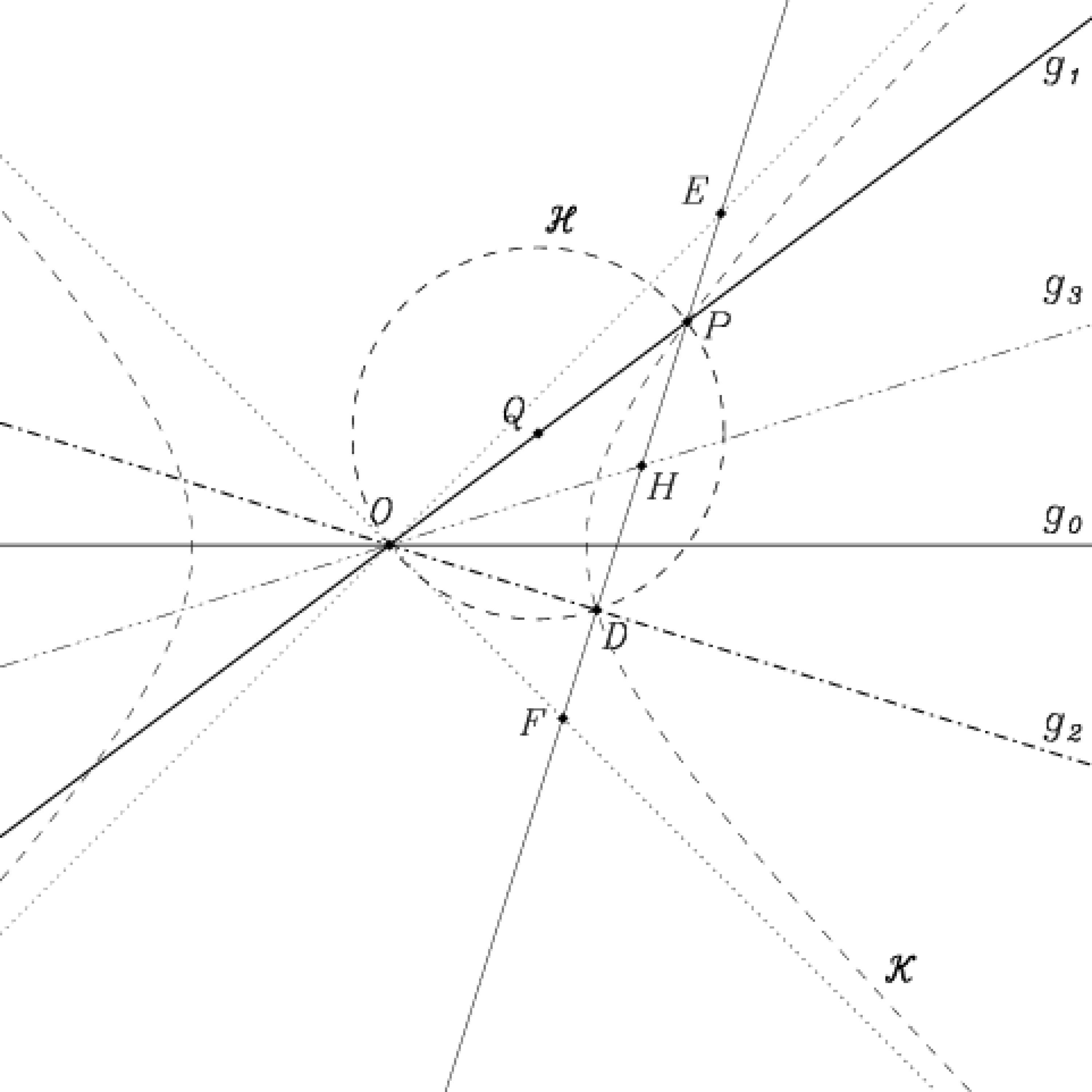
Dreiteilung der Winkels in der pseudoeuklidischen Geometrie
Der Schenkel g0 des Winkel g0g1 wird horizontal gelegt, damit die Spiegelung an ihm euklidisch oder pseudoeuklidisch gleich ist. Ein M-Kreis um O schneide g1 in P. Wir zeichnen einen E-Kreis um den Mittelpunkt Q von OP, der den M-Kreis in D schneidet und halbieren die Strecke PD mit H. Die Schnittpunkte von PD mit den Asymptoten des M-Kreises seien E und F. Man zeigt nun, dass g2 und g3 symmetrisch zu g0 liegen.Dazu benutzt man die Eigenschaft der Hyperbel, dass der Sehnenmittelpunkt H nicht nur PD, sondern auch EF teilt. Dadurch ist nach euklidischem Maß ∠FOD = ∠FEO = ∠HEO wegen der E-rechten Winkel bei O und D, und ∠HEO = ∠HOE wegen der Gleichheit OH = HE. Folglich teilt g0 den Winkel ∠DOH. Nach pseudoeuklidischem Maß teilt H den Winkel DOP, also ist g3 die Lösung der Aufgabe, ein Drittel des Winkels zwischen g0 und g1 nach pseudoeuklidischem Maß zu finden.
Diese Konstruktion ist dual zu der im euklidischen Fall.
zu Kapitel und Portal