11-Punkte-Kegelschnitt der projektiven Geometrie
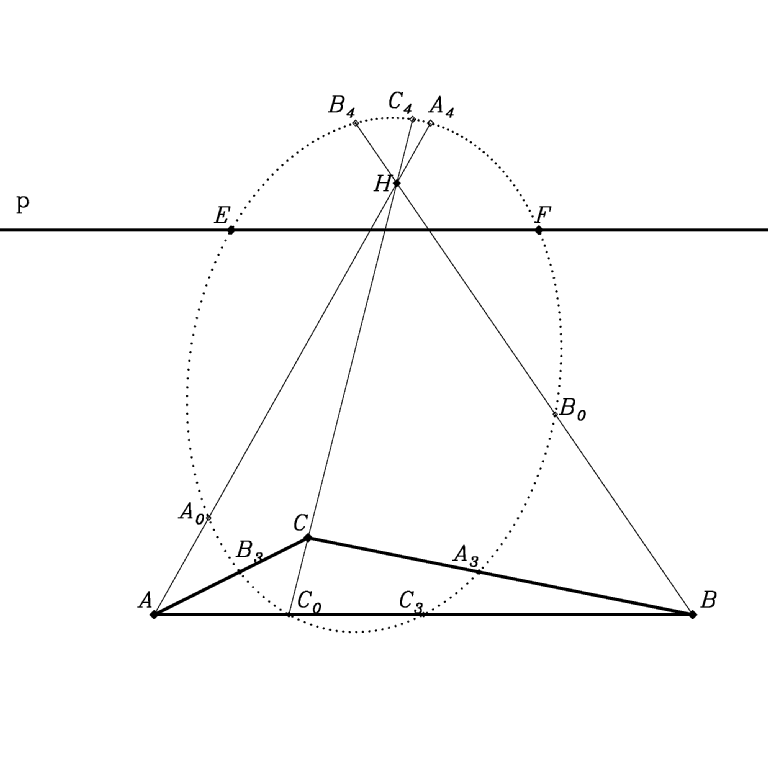
Gegeben sei eine Gerade p mit einem Punktepaar EF. Sie sollen als Ferngerade und Kreispunkte der pseudoeuklidischen Ebeneen dienen. Die Lote auf den Seiten des Dreiecks ABC werden nun über den Schnittpunkt der Seite mit der Ferngeraden bestimmt (wir nennen ihn Fernpunkt der Seite). Der Pol einer Geraden (durch den alle Lote auf ihr gehen) ist der vierte harmonische Punkt zu diesem Schnittpunkt bezogen auf das Punktepaar EF.Die Mitte einer Seite ist der vierte harmonische Punkt zu ihrem Fernpunkt bezogen auf das Eckpunktepaar der Seite. Durch die drei Fußpunkte A0B0C0, die drei Seitenmitten A3B3C3, die drei Höhenmitten A4B4C4 und die beiden Punkte EF geht ein Kegelschnitt, der in die Feuerbachkreise übergeht, wenn p ins unendlich Ferne rückt. E und F sind die absoluten Kreispunkte, die im pseudoeukidischen Fall reell sind (die Asymptotenrichtungen der gleichseitigen Hyperbeln), im euklidischen Fall aber imaginär.
zu Kapitel und Portal