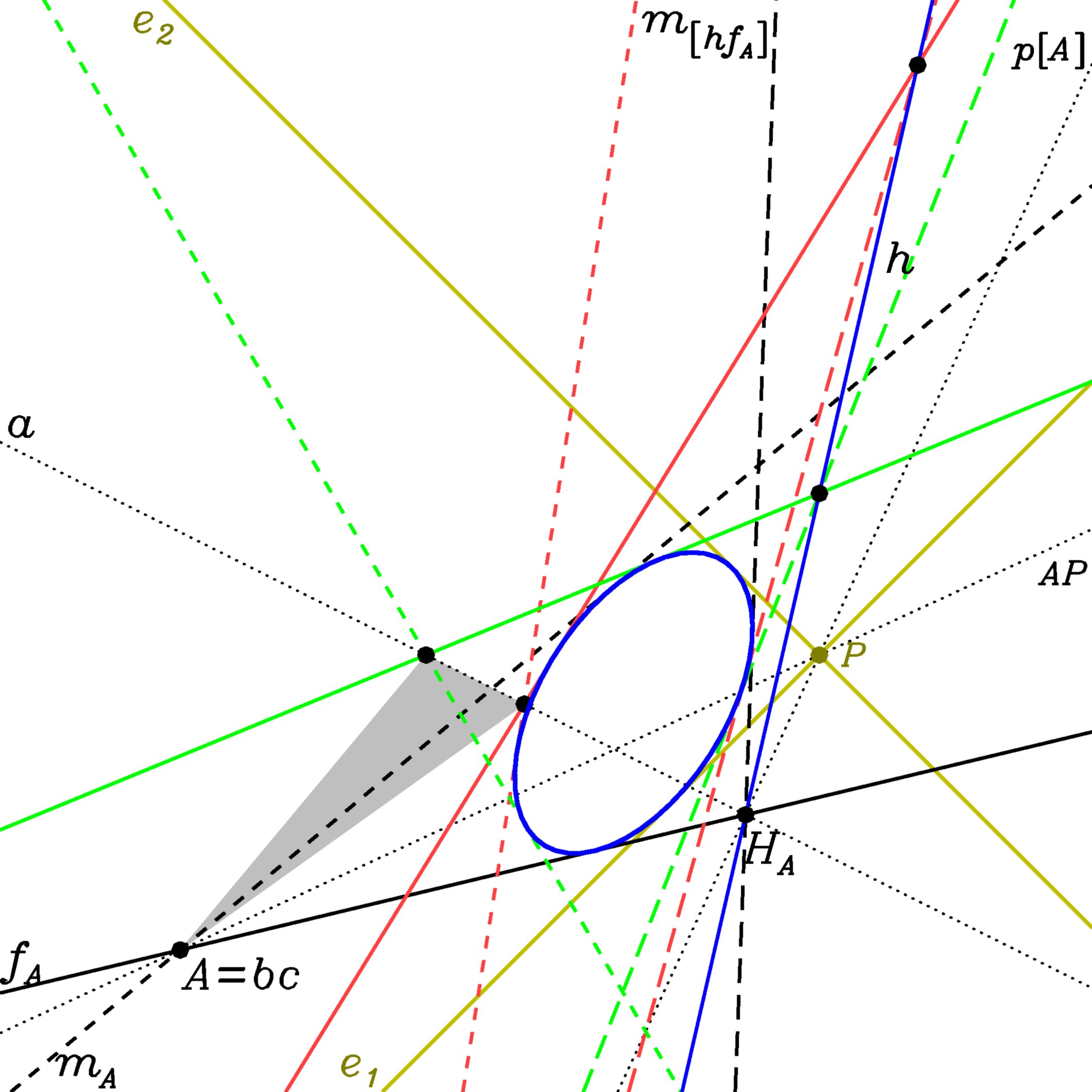
Feuerbachkegelschnitt in der anti-Minkowski-Geometrie,
in der die Metrik durch zwei reelle Geraden bestimmt wird (e1 und e2, Schnittpunkt P). Zu jedem Punkt A gibt es eine Gerade durch P, deren Punkte dualsenkrecht auf A liegen. Ihr Schnitt mit der Seite a ist der zur Höhe duale Punkt. Statt der drei konkurrenten Höhen finden wir nun drei kollineare Höhenpunkte (blaue Linie). Ihre Verbindung mit den drei Ecken (durchgezogene Linien) sind nun Tangenten eines Kegelschnitts, der auch von den sechs Winkelhalbierenden (kurz gestrichelt für A, B, und C, lang gestrichelt für HA, HBHC) tangiert wird. Schließlich gehören auch die absoluten Geraden zu seinen Tangenten. Dieser 11-Tangenten-Kegelschnitt ist dual zum 11-Punkte-Kegelschnitt derMinkowski-Geometrie.
zu Kapitel und Portal