E = m c2: The Geometry of Time
The shortest path from Newton's Laws to the most famous formula in science
is the way through
the geometry on the registration strip of some one-dimensional
(horizontal in the following movies) motion.
It starts at Newton's Laws, implements the Reflection Rule of Light and redraws
the registration of a symmetric decay in flight. Newton's Third Law then states a variation of
mass with velocity, and Newton's Second Law states that the increment in mass is proportional
to the increment in kinetic energy, dEkinetic = dm c2.
Finally: If some part of the energy is proportional to a corresponding part of the mass,
and if the sum of all energies as well as the sum of all masses are conserved,
the total mass and the total energy must be proportional with the same factor,
E = m c2.
The first law of Newton (Galilei's law) states that force-free motion draws a straight
line (straight world-line) on the registration strip. The inclination of this line with respect to
the vertical is the velocity. Hence we know that motions of bodies with
only short interactions (collisions) can be analysed with simple trigonometry.
We unscroll the registration paper so fast that the
inclination of the registration of a photons motion is about 45 degrees. This includes
that spatial (i.e. horizontal) distance is measured by the time that takes the light to pass it.
We use the registration of mechanical reflection to define the geometric reflection procedure
that induces translations and "rotations" on the reflection strip homologously to Euclidean geometry.
The unexpected point is that the everyday experience of reflection as inversion of the
velocity relative to the mirror is not precise enough, because the velocity of light itself
is inverted.
 |
 |
 |
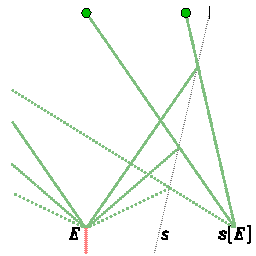
| This movie shows two balls between two reflecting walls, the left one at rest,
the right one in motion. In Newtonian mechanics, the reflection is taken as
inversion of the speed relative to the mirror |
This movie shows the reflections of some fragments of an explosion on a
moving wall. With inversion of the relative velocity, the reflected
world lines intersect at an event always simultaneous to the explosion event. |
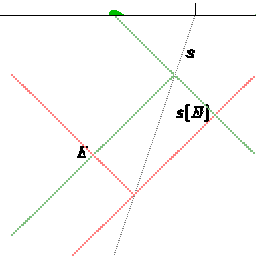
Light does not fit into the Galilean reflection scheme.
The velocity of light is inverted independently
of the motion of the mirror. The reflected image of an event is now constructed
as fourth point in a quadrilateral of lightlike lines. |
Newton's third Law (Huygens' law) tells us that the velocities v have to be weighted
by a factor the depends only on the bodies internal properties, i.e. the (inertial)
mass m, in order to obey a conservation law: The sum of all products mv
remains constant in collisions (interactions in general).
We now consider a moving body that decays into two identical fragments. If the decaying body is at rest,
the fragments move with equal speed in opposite directions. If the decaying body
moves already with this speed, one fragment will remain at rest.
The two world-lines of the fragments must lie symmetrically to the world-line of the
primary body. This must be checked with light. We send a photon from the left that is supposed to be reflected
appropriately by the fragments as well as by the world-line of the decayed object.
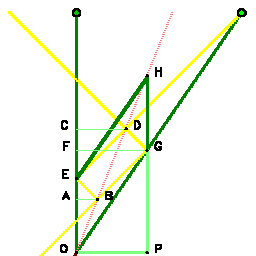
In the figure,
the events E and G lie symmetric to the line
OH because the direction BE is the reflection of the direction BG,
and the direction GD is the reflection of the direction ED.
|
movie |

large figure |
We compare the coordinates of the two points E and G. When FG indicates the velocity, OF is the velocity of light.
When OP = FG indicates the momentum mv of the second fragment,
it is also equal to the momentum of the decaying body, MV.
The first fragment is at rest, it has momentum zero.
Hence, PG is equal to mc, and PH is equal to Mc. The
interval
OE = GH must be the mass of the fragments at rest, m0c
because of the conservation of mass, M = m0 + m.
We obtain the relation m[v]/m0 = PG/OE.
It can be seen that the mass of the moving fragment is larger than the mass
of fragment at rest. The relation of these masses can be found through use of the ordinary
congruence and similarity theorems to yield the known formula
m2c2 - m2v2
= m02c2.
|
Adding some velocity dv, we add the momentum d(mv), and the same formula
yields
(m+dm)2c2 - (mv+d(mv))2
= m02c2.
We subtract the first one and obtain to first order in the small increments
2mc2 dm - 2mv d(mv) = 0.
This is the final clue.
The energy dE added to a body through an accelerating force K is given through Newton's second law, dE = K ds,
yields first dE = (d(mv)/dt) ds, next dE = (d(mv)/dt) ds = d(mv) v
and finally dE = (d(mv)/dt) ds = d(mv) v = dm c2.
When we add up all small contributions from all small acceleration steps, and when we suppose
m = 0 for E = 0, we
obtain E = m c2. |
This is already the complete story. Some comments are appropriate.
|
When we already know, that photons exist, and that the momentum of a photon is proportional to its
energy, mphotonc = Ephoton/c, the conclusion is much shorter.
The simultaneous statement of a conservation law for the energy and a conservation law
for the mass requires that all energy is proportional to inertial mass with the
same factor. |

|
In Newtonian mechanics, reflection-symmetric events are simultaneous. The mirror divides the
connecting interval in equal parts. The simultaneity
reflects the additive composition of velocities
and the independence of mass on velocity as well.
In Einstein's mechanics, reflection-symmetric events in general are no more simultaneous,
masses vary with velocity, and the velocities are composed additively no more.
|
| (Special) Relativity Theory is the application of the space-time geometry defined
by the propagation of light to mechanics of particles, beginning with Newton's laws.
The prediction of antimatter shows that Special Relativity cannot be discarded.
The applicability of SRT is not in doubt as long as the gravitational potential
is small (10-8 on earth). In the gravitational field, some of the
relations that are found must be made more precise, but not given up (General Relativity Theory).
E = mc2
stands unchanged also in GRT.
|
|




