Einige Abbildungen
- Der elastische Stoß
- a2 - b2 = c2
- Parkettierung der Pseudokugel
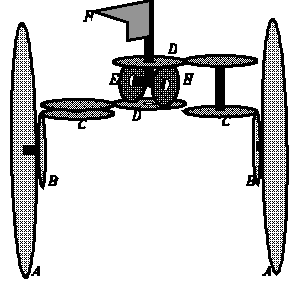
- Dr.Yi-nan Chin gab mir dieses Foto eines Zhi nan che:

Dies ist ein Buch über Geometrie und über Physik.
Es stellt das Wechselspiel der Grundlagen beider
auf neue Art, durch genau konstruierte ebene und perspektivische
Zeichnungen dar.
Die projektive Geometrie ist für den Physiker ein Land voller Wunder.
Ich
habe sie in Vorlesungen von Rudolf Bereis in Dresden kennengelernt, und sie hat mich immer wieder gefesselt. Die Begeisterung war endgültig,
als ich sah, daß die projektive Geometrie einen ganz besonderen Zugang zur
Geometrie der Relativitätstheorie bereitstellt, zu all dem
merkwürdigen Verhalten
von Uhren und Maßstäben, das in der
populärwissenschaftlichen Diskussion immer die meiste Zeit beansprucht.
Die projektive Geometrie ist der gemeinsame Gesichtspunkt, der nun vieles
selbstverständlich, weil homolog zur euklidischen Geometrie,
erscheinen läßt. In dem Buch "Relativitätstheorie mit
Zirkel und Lineal" ist das dargestellt worden. Inzwischen lassen
sich Zeichnungen mit dem Computer sehr viel einfacher herstellen und variieren, so daß es an der Zeit ist, die noch viel
weitergehenden Möglichkeiten der Darstellung der Geometrie
gekrümmter Räume und damit die Anfangsgründe der Allgemeinen
Relativitätstheorie und Kosmologie einzubeziehen und den Zusammenhang
von Physik und Geometrie in größerer Vollständigkeit darzustellen.
Berühmte Physiker und Mathematiker haben sich immer wieder zum
Zusammenhang von Physik und Geometrie geäußert, darunter
Kant,
Helmholtz,
Poincaré,
Einstein und Hilbert.
Jedoch trifft man nur
vereinzelt auf elementare Illustrationen dieser grundlegenden
Frage beider Gebiete. Hier setzt das vorliegende Buch an.
Es stellt die geometrischen Eigenschaften
von Raum und Zeit in den Zusammenhang mit Grundlagen der
Mechanik und Kosmologie. Dabei strebt es
keine vollständige Darstellung der beiden Gebiete an, sondern versucht
die Nahtstelle so zu veranschaulichen,
wie es weder auf der einen noch auf der anderen Seite
gewöhnlich geschieht.
Es setzt keine über den Schulstoff hinausgehenden Kenntnisse von
Geometrie und Mechanik voraus, aber die Offenheit, über das
Angebot nachzudenken und sich anstoßen zu lassen, in die
Gedankenwelt beider Gebiete einzudringen. Mit welcher
Vorkenntnis der Leser das
Buch auch in die Hand nimmt, er wird überrascht sein, wie weit
er bereits auf elementarer Stufe in das jeweils andere Gebiet
hineingreift, und inwieweit das eine Gebiet von dem anderen
abhängt. Der Text ist -- so gut es geht -- von Formalisierung
freigehalten in dem Glauben, daß die Abbildungen das
euklidische
siehe ermöglichen. Der Leser soll
ungestört die ästhetische Seite aufnehmen können. Für das
weitergehende Interesse wird der formale Aspekt in
den Anhängen dargestellt.
Weder Mechanik noch Geometrie sollen von Anfang an
axiomatisch eingeführt werden.
Statt dessen sollen der Weg von einfacheren zu komplizierteren Erfahrungen
nachgezeichnet und nicht nur der gegenwärtige Glaube, sondern auch
einige Zwischenschritte, dargestellt werden, auch wenn diese später
zu korrigieren sind. Um mit Einstein zu sprechen, wird zuerst ein wenig
auf dem Boden herumgeschnüffelt, bevor das hohe Roß der Verallgemeinerung
bestiegen wird.
Für die Freude, die mir die Herstellung des Buches gemacht hat,
ist vielerlei Dank abzustatten, der beim Geometrieunterricht in der
Schule beginnt und bei den Arbeitsmitteln im Institut
endet, Ermutigung, Diskussion und praktische
Hilfe einschließt. Besonders danken möchte ich
E.Quaisser für wichtigen Rat, H.-J.Treder für die vielen Diskussionen
zu den prinzipiellen Fragen des Themas, S.Liebscher für die Unterstützung
bei der Computertechnik und K.Liebscher für ihre Unterstützung und Geduld. J.Barbour und R.Schmidt haben das Manuskript kritisch durchgesehen.
Besonderer Dank gilt S.Antoci, der mit DAOS (Devil's Advocate
Online Service) ein wenig italienischen Geist beigetragen hat, dem der Leser
an verschiedenen Stellen begegnen wird.
Potsdam, im Februar 1999
Inhalt
B.G.Teubner Verlagsgesellschaft, Leipzig und Stuttgart 1999. |
Einige Abbildungen
|

|

|
home to D.-E. Liebscher
mail to D.-E. Liebscher
Last updated: November 6, 1997