zurück zur Hauptseite

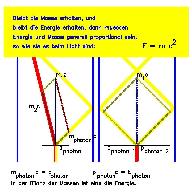
E = mc2: Die Geometrie der Zeit

Der kürzeste Weg zur berühmtesten Formel in der Wissenschaft

führt über die Geometrie auf dem Registrierstreifen einer eindimensionalen (in den folgenden Bildern horizontalen) Bewegung. Er beginnt bei den Newtonschen Axiomen, bezieht sich dann aber auf Reflexionsregel für das Licht und zeichnet die Registrierung eines symmetrischen Zerfalls in Bewegung neu. Newtons drittes Axiom stellt dann die Änderung der Masse mit der Geschwindigkeit fest. Newtons zweites Axiom zeigt, dass die Zunahme an Masse gerade proportional der Zunahme an kinetischer Energie ist, dEkinetisch = dm c2. Am Ende schließen wir:
Wenn ein Teil der Energie proportional zu einem entsprechenden Teil der Masse ist, und wenn die Summe aller Energien ebenso erhalten bleibt wie die Summe aller Massen, muss diese Gesamtenergie mit demselben Faktor proportional der Gesamtmasse sein, E = m c2.
Das erste Newtonsche Axiom (das Galileische Axiom) stellt fest, dass die kräftefreie Bewegung eine gerade Linie (gerade Weltlinie) auf den Registrierstreifen zeichnet. Die Neigung dieser Linie gegen die Vertikale ist die Geschwindigkeit. Wir rollen den Registrierstreifen so schnell ab, dass die Neigung der Weltlinie eines Photons 45 Grad beträgt. Das heißt, die horizontale (räumliche) Entfernung wird durch die Zeit gemessen, die das Licht von einem Ende zum anderen braucht.
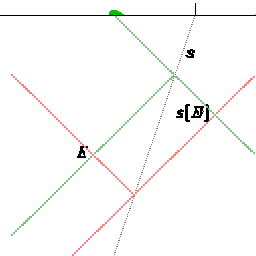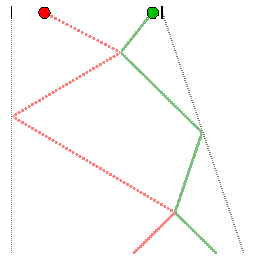
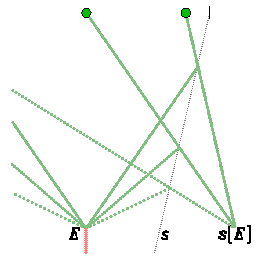
Papierstreifen Explosion Papierstreifen
Dieser Film zeigt zwei Kugeln zwischen reflektierenden Wänden. In der Newtonschen Mechanik ist die Reflexion die Vorzeichenumkehr der Relativgeschwindigkeit Mit der Umkehr der Relativgeschwindigkeit schneiden sich die reflektierten Weltlinien in einem Ereignis s[E], das immer gleichzeitig zum Explosionsereignis ist. Das Licht passt nicht ins Galileische Schema. Die Geschwindigkeit des Lichts selbst ändert das Vorzeichen unabhängig von der Bewegung des Spiegels. Das Spiegelbild eines Ereignisses ergibt sich nun als vierter Punkt eines Parallelogramms aus lichtartigen Linien.
Das dritte Newtonsche Axiom (das Huygenssche Axiom) sagt, dass die Geschwindigkeiten v mit einem Faktor gewichtet werden müssen, der nur von den inneren Eigenschaften der Körper abhängt (das ist die träge Masse m), damit die Summe der so gewichteten Geschwindigkeiten erhalten bleibt: Die Summe aller Produkte mv bleibt bei Stößen (allgemein Wechselwirkungen) unverändert.
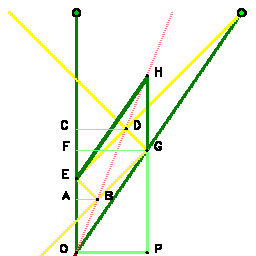
Wir betrachten ein Objekt, das in zwei identische Fragmente zerfällt. Ist das Objekt vorher in Ruhe, streben die zwei Fragmente mit entgegengestetzt gleichen Geschwindigkeiten auseinander. Bewegt sich das Objekt bereits mit dieser Geschwindigkeit, bleibt ein Fragment in Ruhe.
Die beiden Weltlinien der Fragmente müssen spiegelbildlich zur Weltlinie des Ausgangsobjekts liegen. Dies wird mit dem Licht geprüft. In der Abbildung liegen etwa die Ereignisse E und G symmetrisch zur Geraden OH weil die Richtung BE das Spiegelbild der Richtung BG und die Richtung GD das Spiegelbild der Richtung ED ist. 		Impuls Film
movie
Impuls Bild
large figure		 Wir vergleichen nun die Koordinaten der zwei Punkte E und G. Wenn FG die Geschwindigkeit bezeichnet, ist OF die Lichtgeschwindigkeit. So haben wir die Abrollgeschwindigkeit des Registrierstreifens gewählt. Wenn die Strecke OP = FG aber den Impuls mv des zweiten Fragments darstellt, dann ist sie auch gleich dem Impuls MV des bei O zerfallenden Körpers. Das erste Fragment ist in Ruhe, trägt also zum Gesamtimpuls nichts bei. Deshalb ist nun auch PG gleich dem Produkt mc, und PH ist gleich Mc. Die Strecke OE = GH entspricht der Masse m0c des Fragments in Ruhe, und wegen der Erhaltung der Masse ist M = m0 + m. Wir erhalten die Relation m[v]/m0 = PG/OE.
Man sieht sofort, dass die Masse des bewegten Fragments größer als die des ruhenden ist. Kongruenz- und Ähnlichkeitssätze lassen dieses Verhältnis in die bekannte Formel
m2c2 - m2v2 = m02c2.
umrechnen. Nun muß noch der Energiezuwachs nach dem zweiten Newtonschen Axiom dargestellt werden. Dazu addieren wir in der eben erhaltenen Formel noch einen kleinen Zuwachs, das heißt, wir ersetzen v durch v+dv, m durch m + dm und mv durch mv + d(mv). Wir erhalten
(m+dm)2c2 - (mv+d(mv))2 = m02c2.
und ziehen von dieser Gleichung die vorangegangene ab. Dann erhalten wir bei kleinen Zuwächsen 2mc2 dm - 2mv d(mv) = 0.
Das ist der Schlüssel.
Die Energie dE, die einem Körper durch Beschleunigung zugeführt wird, ist nach dem zweiten Newtonschen Axiom dE = K ds, das zunächst in dE = (d(mv)/dt) ds, dann weiter in dE = (d(mv)/dt) ds = d(mv) v und schließlich; in dE = (d(mv)/dt) ds = d(mv) v = dm c2 umgeformt werden kann. Der Zuwachs an kinetischer Energie ist also proportional dem Massenzuwachs. Addieren wir alle kleinen Schritte zusammen, und unterstellen wir m = 0 für E = 0, so erhalten wir E = m c2.




Das ist schon die ganze Geschichte. Wir fügen aber noch einige Bemerkungen an.

Wenn man schon weiß, dass Photonen existieren, dann muss ihr Impuls proportional zur Energie sein, mphotonc = Ephoton/c. Das wissen wir aus der Theorie des elektromagnetischen Feldes und auch aus der Messung des Lichtdrucks. Der Schluss ist dann ganz kurz, weil wir das Argument mit der kinetischen Energie nicht brauchen. Denn ob kinetische Energie oder Photonenenergie, wenn ein Teil der Energie proportional zu einem entsprechenden Teil der Masse ist, und wenn die Summe aller Energien ebenso erhalten bleibt wie die Summe aller Massen, muss diese Gesamtenergie mit demselben Faktor proportional der Gesamtmasse sein. E=mc2
In der Newtonschen Mechanik sind spiegelsymmetrische Ereignisse (etwa E und G) nicht mehr gleichzeitig, die Massen sind von der Geschwindigkeit abhängig und die Geschwindigkeiten setzen sich nicht mehr additiv zusammen.
Die (spezielle) Relativitätstheorie ist die Anwendung der durch die Lichtausbreitung definierten Geometrie von Zeit und Raum auf die klassische Mechanik, beginnend mit den Newtonschen Axiomen. Die Voraussage der Antimaterie zeigt, dass die SRT nicht umgangen werden kann. Die Anwendbarkeit der SRT steht nicht in Zweifel, solange das Gravitationspotential klein ist (auf der Erde ist es etwa 10-8). Im Schwerefeld müssen einige der Begriffe und Beziehungen präzisiert, aber nicht aufgegeben werden (Allgemeine Relativitätstheorie). Die Formel E = mc2 steht unverändert auch in der ART.

Die Newtonschen Axiome
Die Newtonschen Axiome werden im allgemeinen in ihrer geheiligten Form gehandelt. Begriffe wie absoluter Raum (kann man das Gegenteil auch erklären?), Bezugssystem (ganz komplizierte Konstruktion, in der vorausgesetzt wird, was wir erst ableiten wollen), Koordinatentransformation (wo gibt es Koordinaten in der Natur?) werden einfach so benutzt, und gerade bei diesen Begriffen muss viel Erklärungsarbeit geleistet werden. Und wer soll die Tiefe eines Axioms begreifen, das mit unklaren und scheinbar zirkulären Begriffen daherherkommt, etwa: Kräftefreie Bewegung ist geradlinig gleichförmig, aber nur in einem Inertialsystem, und ein Inertialsystem ist dadurch definiert, dass kräftefreie Bewegung dort geradlinig gleichförmig ist usw.
Es ist eben nicht so, dass Newton seine Axiome endgültig formuliert hat, auch er hat um Formulierung und Deutlichkeit (manchmal auch Undeutlichkeit) gekämpft und sie nur im Stile seiner Zeit machen können. Ob eine Bewegung geradlinig gleichförmig ist, kann, ja darf von der Beschreibungsform (den Koordinaten oder Bezugssystemen) nicht abhängen, denn die sind ja gerade menschliche Willkür. Besonders heftig schlagen die Bezugssysteme in den Einführungen in die Relativitätstheorie zu. Dabei wird gerade Vieles einfacher, wenn man darauf verzichtet, sie in den Vordergrund zu schieben, und dafür das zu verwenden, was man inzwischen an anderer Stelle, in der Geometrie, gelernt hat. Die auf diesen Seiten vorgestellte Ableitung der Formel E = m c2 kommt ohne Transformation von Bezugssystemen aus.
Das erste Newtonsche Axiom (die Idee ist von Galilei, wenn man die undokumentierten, aber erschließbaren Kenntnisse der Mathematiker zwischen Euklid und Archimedes vergisst) muss heißen: Die Gesamtheit der unbeeinflussten Bewegungen zeichnen in Raum und Zeit eine Geradenschar. Bezugssysteme kommen noch gar nicht vor, müssen es auch nicht. Auch das Wort kräftefrei sollte vermieden werden, denn Kraft wird später genauer definiert. Geraden sind eben nicht über Koordinaten definiert, sondern durch ihre Eigenschaft, sich höchstens einmal zu schneiden, und durch zwei verschiedene Punkte eindeutig definiert zu sein. Das ist alles. Koordinaten kommen nun erst hinein, weil man zu einer Geradenschar immer Koordinaten (eben ein Bezugssystem) finden kann, indem die Geraden durch lineare Beziehungen beschrieben werden. Diese Bezugssysteme sind lineare Bezugssysteme (noch keine Inertialsysteme), und die erlaubten Koordinatensubstitutionen sind die linearen, keineswegs eingeschränkt auf die Galilei- oder Lorentz-Transformationen.
Das zweite Newtonsche Axiom gehört logisch erst an die dritte Stelle. Es führt die Begriffe Masse und Kraft gemeinsam ein, obwohl der Begriff der Masse fundamentaler ist und der Analyse des Begriffs Kraft nicht bedarf. Grundlegender ist das dritte Axiom, das eigentlich an die zweite Stelle gehört, aber eben in einer Form, die auch nicht von Newton stammt, sondern von Huygens (mit der gleichen Einschränkung wie bei Galilei). Bei einer Wechselwirkung bleibt die Summe der Geschwindigkeiten konstant, wenn sie vorher gewichtet wurden. Die Wichtung nennen wir Masse, die gewichteten Geschwindigkeiten Impulse. Und: Die Summe der Massen bleibt konstant. Man sieht: Über Kräfte muss noch gar nichts gesagt werden. Gerade deshalb kommt dieses Axiom vor dem zweiten. Es begründet auch ohne weiteres, dass das zweite nun über die Änderung des Impulses reden muss, und nicht über Beschleunigungen.
Wenn ohne äußere Einwirkung der Impuls erhalten bleibt, dann muss diese Einwirkung, die wir Kraft nennen, die Änderung des Impulses bewirken. Also: Die Kraft ist gleich der Änderung des Impulses pro Zeit. Wenn mann nur die Impulsänderung messen kann, definiert dieser Satz die Kraft, aber sie ist dann eben definiert. Auf andere Objekte übertragen, bestimmt er die Bewegung. Auch die Kraft unterliegt dem 3. (Huygensschen) Axiom. Aus diesem folgt, dass in dem Spezialfall, wo die Kräfte nur von der Lage und den Eigenschaften zweier Körper abhängen, die gegenseitigen Kräfte entgegengestzt gleich sein müssen, weil sich sonst die Summe der beiden Impulsänderungen nicht Null ist, wie das dritte Axiom fordert. Newtons große Leistung besteht darin, gesehen zu haben, dass ein Kraftgesetz der Form K12 = G M1M2R12-1 die Keplerschen Gesetze erklärt. Es hat in der Folge soweit geführt, die Wiederkehr des Halleyschen Kometen zu bestimmen, die von Piazzi entdeckten kleinen Planeten wiederzufinden und die Störungen des Planeten Uranus auf einen ferneren Planeten (den Neptun) zurückzuführen und dessen Bahn und Stellung zu berechnen, so dass er gefunden werden konnte. Auf das Kraftgesetz war er zu Recht stolz, und deshalb hat er es auch an die zweite Stelle seiner Axiomenliste gestellt, obwohl es nach dem Gang der Logik dort nicht hingehört.
Das 3. (Huygenssche) Axiom führt mit der Masse auch das Maß in die Geometrie ein. Der Kreis ist nun definiert als das Ergebnis eines symmetrischen elastischen Stoßes, wenn nach einer bestimmten Zeit die Positionen der Stoßpartner markiert werden. Die Bezugssysteme, in denen dieser Kreis die übliche Gleichung x2+y2+z2=r2 erfüllt, der Satz des Pythagoras also die übliche Form hat, nennen wir Inertialsysteme. Der Satz des Pythagoras definiert die Länge. Substitutionen neuer Koordinaten führen nur dann wieder zu diesen Gleichungen, wenn es Galilei- bzw. Lorentz-Transformationen sind. Welche nun richtig ist, hängt von der beobachteten Spiegelung (Reflexion) ab. Kann man die Spiegelung so beschreiben, dass die Relativgeschwindigkeiten das Vorzeichen wechseln, werden es die Galilei-Transformationen. Sieht man, dass das Licht das Vorzeichen seiner Geschwindigkeit unabhängig von der Bewegung des Spiegels wechselt, werden es die Lorentz-Transformationen. Ob die Natur mitspielt, das heißt, ob diese Gesetze und ihre Folgerungen sich so wiederfinden, ist eine Frage der Beobachtung.
Das Relativitätsprinzip
Der Name Relativitätsprinzip ist zunächst ausgesprochen einschüchternd. Es ist aber nichts anderes gemeint als die Erwartung, dass Galileis Beobachtung (dass geradlinige gleichförmige Bewegung - wie auch Position, Orientierung und Zeitpunkt - eines abgeschlossenen und abgeschirmten Raums in Innern nicht festgestellt werden kann, wie fein auch die Messapparaturen seien, die ich zur Verfügung habe) uneingeschränkt gilt. Geschwindigkeit, Position, Orientierung und Zeitpunkt können nur bezogen auf andere, äußere Objekte (Schlaglöcher, Starkästen, Sterne, kosmische Hintergrundstrahlung) benannt werden.
Die tägliche Erfahrung ist, dass sich bei Reflexion das Vorzeichen der Relativgeschwindigkeit zum Spiegel ändert und diese Relativgeschwindigkeit einfach eine Differenz ist, und dass die Länge eines Zeitintervalls immer die gleiche ist, unabhängig davon, wie die vergleichende Messung zustandekommt. Die daraus folgende Mechanik war so erfolgreich, dass man auch versuchen musste, die Lichtausbreitung mit ihr zu beschreiben. Man fand schnell heraus, dass man ein Trägermedium unterstellen muss (wie die Luft beim Schall) und dass dieses ungehindert durch geschlossene Türen und Wände strömen muss, wenn sich das Zimmer bewegt. Und jedes Zimmer bewegt sich: mit der Erde um die Sonne, mit 30 Kilometer pro Sekunde! Diese ungehinderte Strömung musste unterstellt werden, weil sonst ein Widerspruch zur Aberration der Sterne entstünde. Die Beobachtung der Aberration der Sterne war der große Erfolg der Newtonschen Vorstellung, dass das Licht ein Teilchenstrom ist, der von der Lichtquelle ausgeht. Dann muss man die Geschwindigkeit des Lichts mit der des Beobachters zusammensetzen und erhält eine scheinbare Verschiebung des Sterns in Bewegungsrichtung der Erde, die im Jahresmetrum wechselt, so dass die Sternörter eine Ellipse beschreiben. Die Beobachtung dieses Effekts bestätigte Newtons Vorstellung vom Licht und darüber hinaus die Bewegung der Erde um die Sonne. Die hundert Jahre später notwendige Beschreibung des Lichts durch Wellen enthielt die Aberration zunächst nicht. Erst der Kunstgriff mit dem frei fließenden Äther konnte sie für die üblichen Teleskope wieder erklären.
Die ungehinderte Strömung des Äthers schien nun auch für einen abgeschlossenen Raum die Möglichkeit zu geben, die Geschwindigkeit wenigstens gegen diesen Äther feststellen zu können. Aber das geht nicht, man findet keine Bewegung gegen den Äther. Man kann diese Beobachtung nun zu verschiedenen Schlüssen benutzen. Erst nachdem Lorentz festgestellt hatte, dass die Aberration auf eine Relativität der Gleichzeitigkeit deutet, konnte Einstein sehen, dass das Licht eine neue Regel der Reflexion verlangt: Bei Reflexionen ändert die Lichtgeschwindigkeit das Vorzeichen (die Richtung), nicht aber den Betrag, und dies unabhängig von einer Bewegung des Spiegels. Das ändert die Geometrie der Zeit, ändert die Zusammensetzung der Geschwindigkeiten, macht die Massen geschwindigkeitsabhängig, und ersetzt Galilei- durch Lorentz-Transformationen. Die Unterstellung eines Äthers wird nicht nur überflüssig, sondern auch irreführend.
zurück zur Hauptseite