|
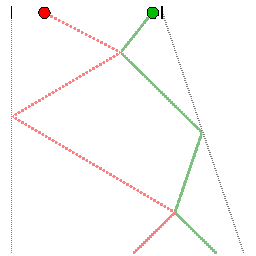
Die Orts-Zeit-Ebene entsteht (Film 250 kB) als Ausgabe eines Streifenregistriergerätes. Hier stoßen zwei Kugeln auf einer Schiene gegen die Wände und miteinander. Zwischen den Stößen sind die Bewegungen kräftefrei und gleichförmig und ergeben auf der Streifenregistrierung Geraden. |

|
Längenvergleich und Winkelvergleich werden durch die Spiegelung definiert. Wir kennen die Entstehung des Kreises (Film 250 kB) im angewinkelten Toilettenspiegel. |

|
Die Spiegelung von (Film 250 kB) Explosionsfragmenten an einem bewegten Spiegel definiert die Spiegelung in der Galilei-Geometrie der klassischen Mechanik: relative Geschwindigkeiten ändern das Vorzeichen. |

|
Drehen wir die spiegelnde Gerade um einen festen Punkt, muss das Spiegelbild auf einem Kreis um den Drehpunkt laufen. Der Kreis der Galilei-Geometrie ist eine Gerade (Film 250 kB). Der Abstand d[M,A]=d[M,s[A]] wird allein durch die Zeitdifferenz bestimmt. Gleichzeitige Ereignisse müssen daher den Galilei-Abstand Null haben: Genau auf den horzontalen Geraden sind die Abstände null. Der Winkel alpha=s[alpha] ist hier identisch mit der Relativgeschwindigkeit der durch die Schenkel des Winkels dargestellten Bewegungen. |

|
Die Spiegelung von Wellen (Film 250 kB) an einem bewegten Spiegel definiert die Spiegelung in der Minkowski-Geometrie der (speziellen) Relativitätstheorie: die Lichtgeschwindigkeit ändert ihr Vorzeichen, nicht aber den Betrag. Die Lichtgeschwindigkeit ist absolut. Die Bewegung des Spiegels ist unerheblich. E und s[E] sind gegenüberliegende Ecken eines sogenannten Lichtecks, dessen anderes Eckenpaar auf dem Spiegel liegt. |

|
Drehen wir die spiegelnde Gerade um eine der Ecken des Lichtecks, so sehen wir, dass jetzt auf den Geraden zweier Richtungen die Abstände null sind (Film 250 kB): Alle d[M,s[A]] sind gleich, also null, und sie sind gleich dem Abstand d[M,A], der also auch null ist. |

|
In der euklidischen Ebene sind Quadrate definiert als Rechtecke, deren Diagonalen einen rechten Winkel bilden. Dann ist die Summe (Film 250 kB) der Flächen der Kathetenquadrate gleich der des Hypotenusenquadrats |

|
In der Orts-Zeit-Ebene sind Quadrate definiert als Rechtecke, deren Diagonalen die Lichtgeschwindigkeit beschreiben. Dann ist die Differenz (Film 250 kB) der Flächen der Kathetenquadrate gleich der des Hypotenusenquadrats |

|
Dieses Bild zeigt den Unterschied zwischen dem Hypotenusenquadrat
in der euklidischen Ebene und dem in der Orts-Zeit-Ebene.
In der Orts-Zeit-Ebene gilt
(AB)2 = (AC)2 - (CB)2. Die längs (AB) ablaufende Eigenzeit ist kleiner als die längs (AC) |

|
Setzen wir zwei solche Dreiecke zusammen, entsteht ein Bild, in dem die Strecke
AD die Registrierung einer ortsfesten Uhr und ABD
die Registrierung einer zweiten Uhr ist, die sich in A
von der ersten entfernt, in B umkehrt und in D
wieder mit der anderen verglichen werden kann. Auf dieser Uhr ist weniger
Zeit abgelaufen, weil die Länge von ABD
kürzer als die von AD ist.
AB ist als Hypothenuse kürzer als AC. BD ist als Hypothenuse kürzer als CB. Nicht ganz symmetrisch dazu ist: AE ist als Hypothenuse kürzer als AB. FD ist als Hypothenuse kürzer als BD. |

|
Auch den Kreis der Orts-Zeit-Ebene erhalten wir durch Drehung der spiegelnden Geraden um einen festen Punkt (Film 250 kB). Der Kreis hat jetzt nicht mehr die Gestalt einer Ellipse, wie in der euklidischen Ebene, sondern die einer Hyperbel: immer noch ein Kegelschnitt, jetzt aber einer mit zwei Punkten im Unendlichen. |

|
Was für Spiegelungen kann man überhaupt definieren? Damit man damit rechnen kann, dass Längen und Winkel bei Spiegelung unverändert bleiben, müssen sich die Mittelsenkrechten eines Dreiecks immer in einem Punkt schneiden. Dann schneiden sich auch alle Lote einer Geraden in einem Punkt, dem Pol (Film 250 kB) der Geraden, der in unseren drei Fällen immer im Unendlichen liegt |

|
Ist zu einer Geraden s der Pol P[s] bekannt, kann die Spiegelung mit dem Lineal konstruiert werden. Der Fußpunkt des von einem Punkt A auf den Spiegel s gefällten Lotes teilt mit dem Pol des Spiegel die Strecke von dem Punkt A zu seinem Spiegelbild s[A] harmonisch: Wenn B dieses Spiegelbild sein soll, zeichne ich ein Viereck (Film 250 kB) mit dem Pol P[s] als einem Diagonalpunkt und einem anderen Diagonalpunkt C auf s. Dann muss auch der dritte Diagonalpunkt auf P[s] liegen. Solange dies nicht der Fall ist, kann B nicht Spiegelbild von A sein. |
-

Auf den Tangenten sind die Abstände null (Film 250 kB). Alle Strecken [M,s[A]] sind untereinander gleich und gleich der Strecke [M,A]. Also haben alle diese Strecken die Länge Null. -

Auf dem Kegelschnitt schneiden sich die Geraden mit dem Winkel Null (Film 250 kB): Der Winkel bei s[U] ist immer gleich und immer gleich dem bei U. Also sind beide null. Zwei Geraden, die sich im Unendlichen (d.h. auf dem absoluten Kegelschnitt) schneiden, sind parallel.
- Durch einen Punkt kann es zu einer Geraden keine, eine oder zwei Parallelen geben.
- Auf einer Geraden kann es zu einem Punkt keinen, einen oder zwei Punkte mit dem Abstand null geben.
| Neun Geometrien | Zu den Geraden keine Parallelen | Zu den Geraden eine Parallele | Zu den Geraden zwei Parallelen |
| Auf den Geraden keine Punkte mit Abstand null | Sphärische Geometrie (elliptische Geometrie) | Euklidische Geometrie | Hyperbolische Geometrie (nichteuklidische G. von Bolyai und Lobatschewski) |
| Auf den Geraden ein Punkt mit Abstand null | Anti-euklidische Geometrie | Galilei-Geometrie | Anti-minkowskische Geometrie |
| Auf den Geraden zwei Punkte mit Abstand null | anti-hyperbolische Geometrie | Minkowski-Geometrie (pseudo-euklidische Geometrie) | doppelt-hyperbolische Geometrie (deSitter-Geometrie) |