Ein Ausflug zu den Wundern der nichteuklidischen Geometrie

In der projektiven Geometrie wird das Unendliche zum gewöhnlichen Gegenstand und nur dort kann über das Unendliche etwas Anschauliches ausgesagt werden. Zum Vortrag wird ein Java-Programm benutzt, dessen zweite Version (080508) man sich hier ansehen kann Wo schneiden sich Parallelen? Am Horizont, im Unendlichen? Was sind Parallelen? Wo schneiden sich Geraden, die sich noch nicht einmal am Horizont treffen? Mit der Technik der Projektion finden sich merkwürdige Antworten. Da gibt es nicht nur Punkte jenseits des Unendlichen, sie haben auch Bedeutung für gewohnte geometrische Figuren, und jenseits des Unendlichen wird die zweidimensionale Ebene zu einer Orts-Zeit-Ebene, einem Abbild der Geschichte des Universums.
Wenn wir das Unendliche einer gewohnten Ebene ins Gesichtsfeld bringen wollen, steigen wir auf einen Turm und haben dann das Unendliche als Horizont (Ferngerade) vor Augen. Die Ebene wird ins Gesichtsfeld projiziert, das Projektionszentrum ist unser Auge oder das Objektiv unseres Fotoapparates. Das Foto ist eine Karte des Raums und speziell unserer Ebene. Wir können die originalen Maße nicht mehr unmittelbar mit dem Lineal bestimmen, aber wir können sie erschließen, wenn wir mit den Gesetzen der Projektion zurückrechnen. Das Foto des Potsdamer Hotels Mercure kann etwa verwendet werden, um auf dreidimensionale Verhältnisse zurückzurechnen, mit diesen zu spielen und dann wieder zu projizieren. So ist der Film berechnet, der die Öffnung der Hülle des LBT simuliert
Wenn wir die gewohnte Zeichenebene so projizieren, dass wir den Horizont sehen, so erscheint dieser als gerade Linie, als Ferngerade, auf der sich parallele Geraden wirklich schneiden. Mit der geradentreuen Projektion sehen wir auf dem Zeichenblatt nie die gesamte Ebene. Mit einer Projektion, die zunächst aus dem Mittelpunkt einer aufgesetzten Kugel auf die Kugelfläche und dann aus deren Nordpol auf die Ebene zurück projiziert, erhalten wir einen Kreis, in dessen Innerem jeder Punkt der Ebene ein Abbild findet. Die Geraden der Ebene sind jetzt Kreisbögen zwischen gegenüberliegenden Punkten der Peripherie.
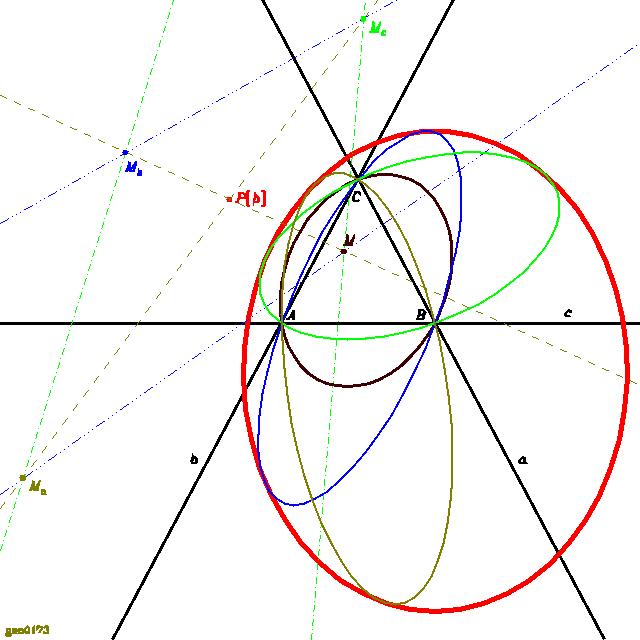
Kann man die Schlussformen der gewohneten Geometrie anwenden, wenn man in dem gegebenen Kreis die gewohnten Geraden benutzt? Das wird die Geometrie ohne Parallelenaxiom, die viele Jahrhunderte gesucht und vor knapp 200 Jahren von Lobachevski und Bolyai gefunden wurde. Es gibt nun Geraden, die sich nicht einmal im Unendlichen (hier durch die Kreisperipherie dargestellt) schneiden: Sie schneiden sich jenseits des Unendlichen. Die geometrischen Formen werden mit Hilfe des Kreises konstruiert, der bei allen Spiegelungen sein eigenes Spiegelbild sein muss. Im Kleinen finden wir die gewohnten Zusammenhänge. Im Großen löst sich u.a. die Merkwürdigkeit, dass es zu zwei Geraden zwei Winkelhalbierende gibt, zu einer Strecke aber scheinbar nur einen Mittelpunkt, dass es zu einem Dreieck vier Kreise gibt, die die Seiten berühren, aber scheinbar nur einen, der durch die drei Eckpunkte geht. Die zweite Seitenmitte und die Mittelpunkte der drei fehlenden Kreise liegen jenseits des Unendlichen.
Das Gebiet jenseits des Unendlichen ist ein Modell des leeren Universums, wie es zuerst de Sitter untersucht hat, und wie es wohl auf die ferne Zukunft des Universums passt. Anders als innerhalb des Grenzkreises gibt es Linien, auf denen alle Strecken die Länge Null haben, Umwege sind jetzt kürzer als die direkten: die Lichtausbreitung und das Zwillingsparadoxon lassen grüssen. Im Kleinen finden wir nun die Zusammenhänge von Raum und Zeit, wie sie in der speziellen Relativitätstheorie aufgeklärt werden. Um die Gesetze der Perspektive nutzen zu können, haben wir ausschließlich geradentreue Zeichnungen verwendet. 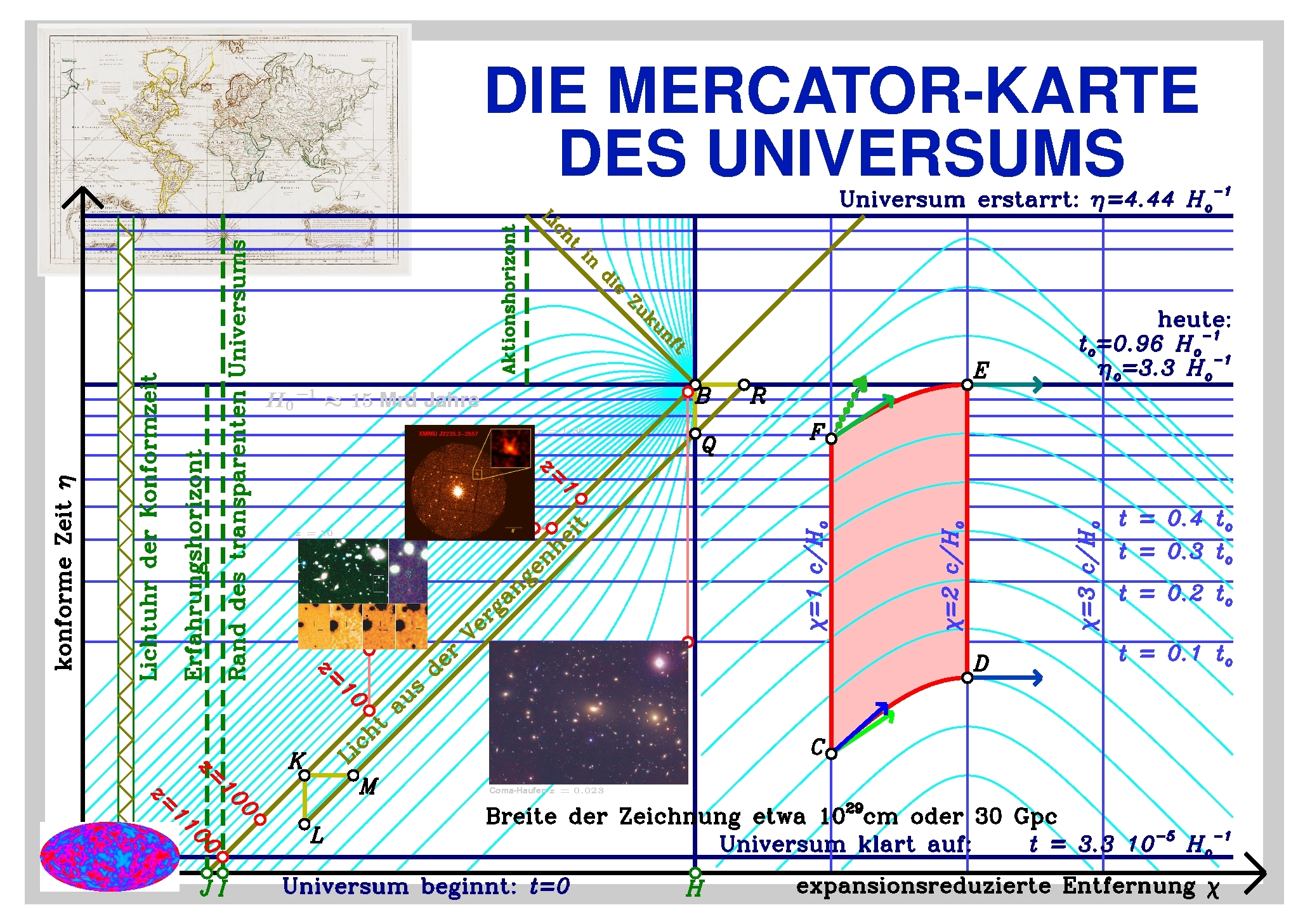Für die Geschichte des Universums ist eine winkeltreue Darstellung besser geeignet. Die winkeltreue Darstellung zeigt, dass wir heute schon Galaxien in einer Entfernung sehen, zu der die Signale, die wir heute und in Zukunft geben können, und die Emissäre, die wir heute und in Zukunft entsenden k&puml;nnen, nie mehr gelangen. Der Teil des Universums, den wir überblicken, wird sich von heute an etwas mehr als verdoppeln, der Rest bleibt auf ewig unsichtbar.