|
|
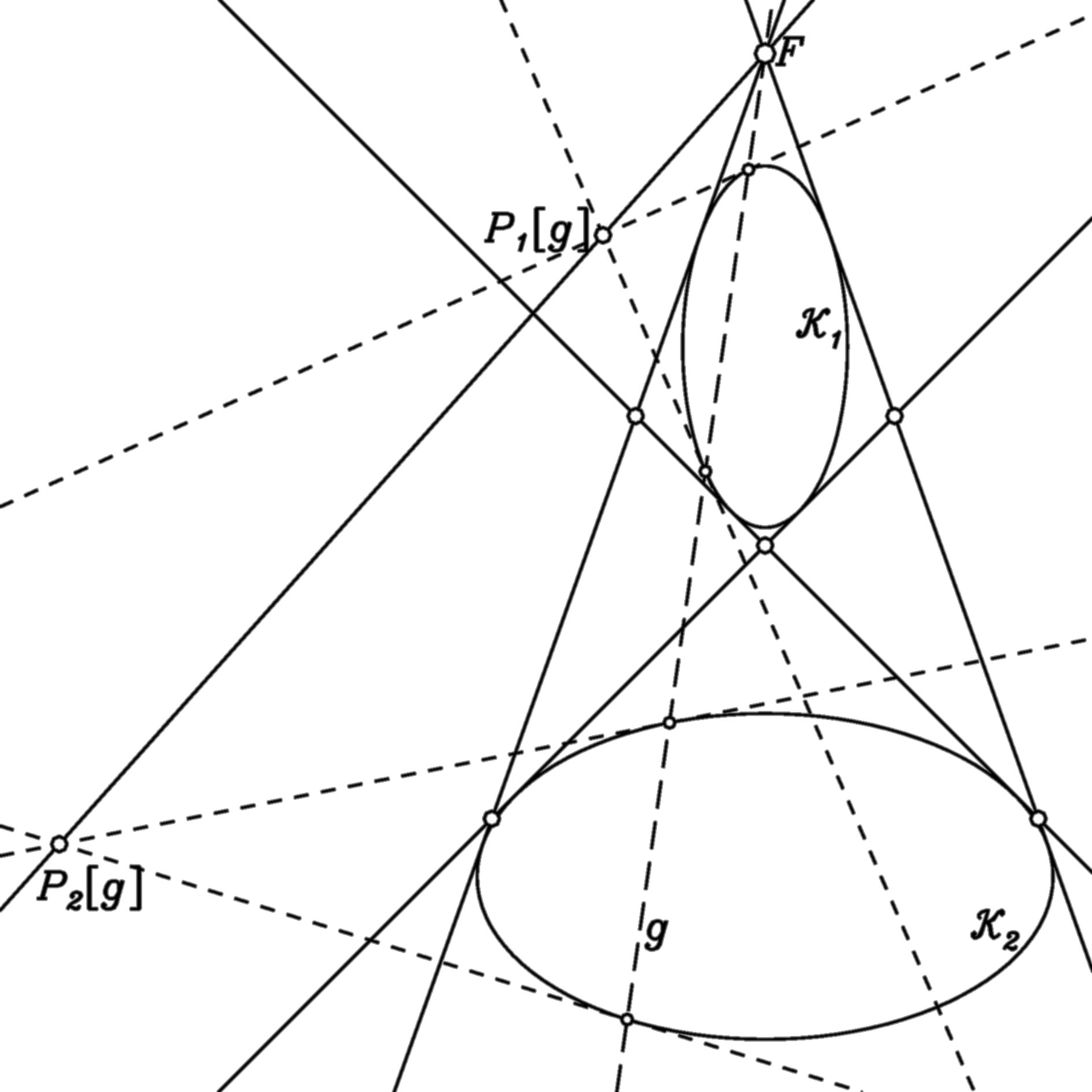
Foci of conics in non-euclidean geometry
Two conics define four common tangents (not necessarily real) and three pairs of intersections called foci. When the two conics do not intersects,
the four tangents and the six foci are real.
Any line g through a focus F has two poles P[g] with respect to the two conics. The two poles and the focus are collinear.
The line of these three point divides with g the two tangents through F harmonically.
This reproduces the familiar property of foci in euclidean geometry.
|







